圆周角定理及推论证明(熟练掌握圆周角定理)
抽丝剥茧,详细解析初中数学题386
386:如图所示,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠C。
⑴求证:CB∥PD
⑵若BC=3,sin∠P=3/5,求⊙O的直径。
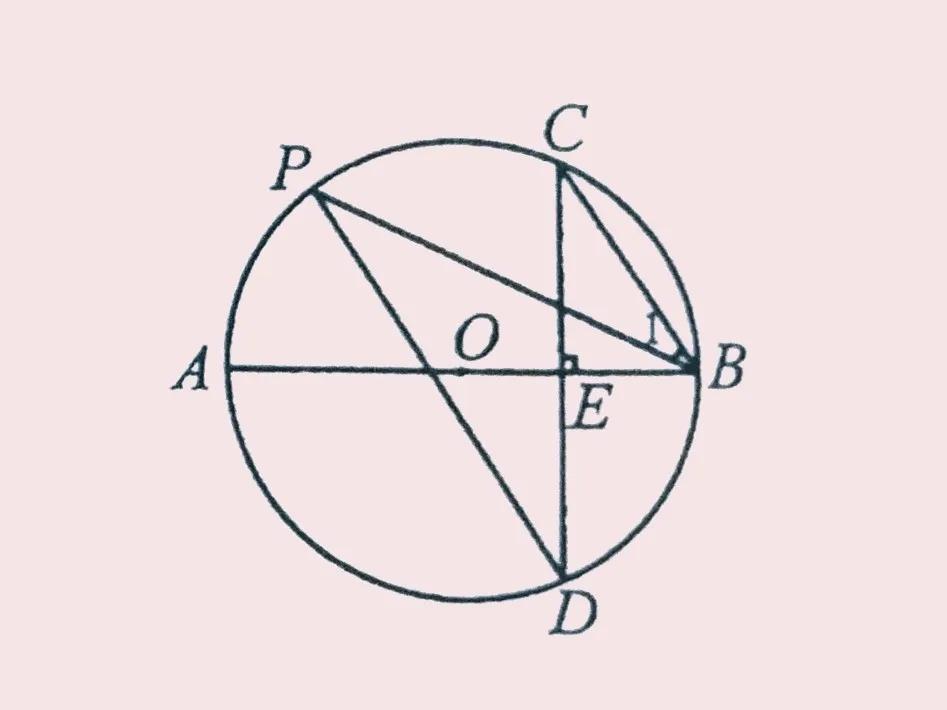
解析:1.证明CB∥PD很简单,
∵∠P=∠C,∠1=∠C,
∴∠P=∠1,
∴CB∥PD(内错角相等)。
2.因为有已知条件sin∠P=3/5,
而∠P=∠BCE,
所以sin∠BCE=3/5;
又因为直径AB⊥CB,
再把AC连接起来,
就将问题放在Rt△ACB中去进行了,
如下图所示,
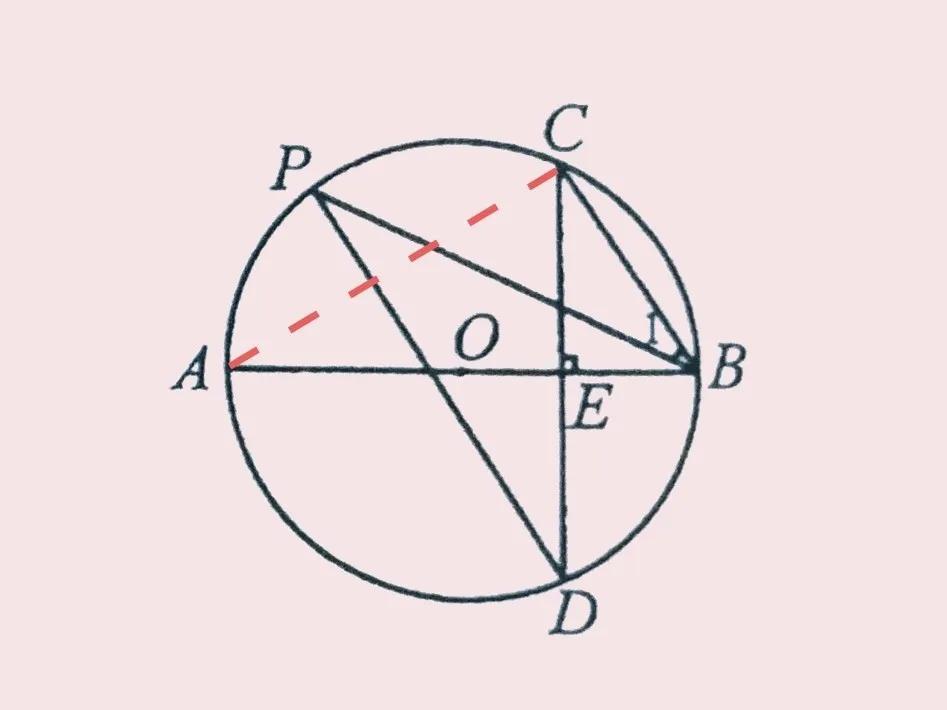
∵∠BCE=∠CAB,
∴sin∠CAB=3/5,
又BC=3,
∴AB=BC/sin∠CAB
=3/3/5=5。
小结:圆周角定理及其理论
1.圆周角定理:圆上—条弧所对的圆周角等于它所对的圆心角的一半。
2.推论:
①同弧或等弧所对的圆周角相等;
同圆或等圆中,相等的圆周角所对的弧也相等。
②直径所对的圆周角是直角;
90°的圆周角所对的弦是直径。
相关文章
-
《方舟指令》被批除了立绘其他的都是什么东西!
最近被安利了一款叫做《方舟指令》的少女养成游戏,这款游戏宣传非常的不错,听说下载这款游戏会或的B站的会员,这小编就一定要试试了! 《方舟指令》的故事背景比较中二,科技发达到2353年,契灵成为这个世界最常见的东西,这是一个竞技少女原型人形化身。科技界限被突破后,是再创更高的文明还是遵循自然法则毁灭
2025-04-03 07:44:18
-
耐看的王道冒险故事——《勇者斗恶龙10离线版》
一次还算不错游戏体验,还是希望呈现更多诚意。【评测前言】 说到RPG,那一定会想到由日本艾尼克斯(现为史克威尔艾尼克斯,也称SE)开发制作,享有日本“国民级RPG”美称的《勇者斗恶龙》系列。 作为游戏史上最畅销的长寿游戏之一,《勇者斗恶龙》第一代发售于1986年5月27日,故事由堀井雄二主理,椙
2025-04-03 06:33:57
-
《原神》赛索斯等级突破材料一览
《原神》赛索斯等级突破材料一览20级突破材料:最胜紫晶碎屑1个、褪色红绸3个、20000摩拉;40级突破材料:最胜紫晶碎断片3、凝云鳞甲2个、万相石10个、褪色红绸15个、40000摩拉;50级突破材料:最胜紫晶碎断片6、凝云鳞甲4个、万相石20个、镶边红绸12个、60000摩拉;60级突破材料:最
2025-04-03 03:40:20
-
死锁Deadlock跳ping?出现这种情况不要慌,来看。
在《死锁Deadlock》这款竞技游戏中,跳ping是许多玩家面临的棘手问题。它不仅影响游戏体验,还可能直接导致战斗失利。不过,别担心,以下将为你介绍三个解决步骤,帮助你稳定游戏连接,享受流畅对战。第一步:检查并优化你的网络环境首先,面对该游戏的跳ping问题,你需要从源头出发,检查并优化自己的网络
2025-04-02 12:15:12
-
《迷雾大陆》平民流派搭配辅助攻略
一、德鲁伊辅助技能搭配在S3赛季中,德鲁伊的核心技能主要用于增伤,帮助队友提高输出。以下是几个推荐技能:岩刺-腐蚀:这是德鲁伊的基础技能组合,可以有效地对敌人造成持续伤害,并为队友提供伤害增益效果。枭兽之力-震荡波-地陷:这组技能可以触发腐蚀效果,并与相关装备配合产生高额输出,适合群体作战。荆棘光环
2025-04-02 08:21:24
-
明日方舟新手干员推荐指南高效养成与策略搭配
推荐理由:免费获取于活动“覆潮之下”,费用低廉,精一即带自回血,未来可融入深海猎人体系。注意:六星养成成本较高,需适度投入资源。2. 阿米娅(五星 术士 中坚术士/五星 近卫 术战者)推荐理由:游戏初期即赠,第八章关键角色,精二后解锁真伤形态,双重职业体验。注意:技能使用有限制,需合理规划。3. 幽
2025-04-02 07:26:12



