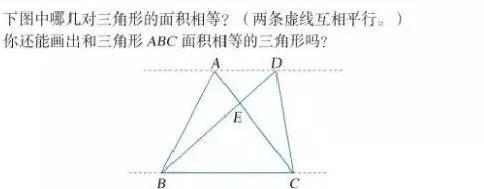
垂线段的定义（［证明面积相等的三大方法］）

☞适用条件:在三角形和平行四边形中，有一些特殊的线，比如中线、对角线、垂线以及平行线（以上简记为“四线”）都会分割出一些面积相等的图形出来。如果牢记“四线”特性，会帮助我们第一时间找出面积相等关系。

❶中线:中线能把三角形的面积（S）分为相等的两部分，每一部分面积为S÷2。［中线定义:在三角形中，连接一个顶点和它所对的边的中点的线段叫做三角形的中线］

例如:

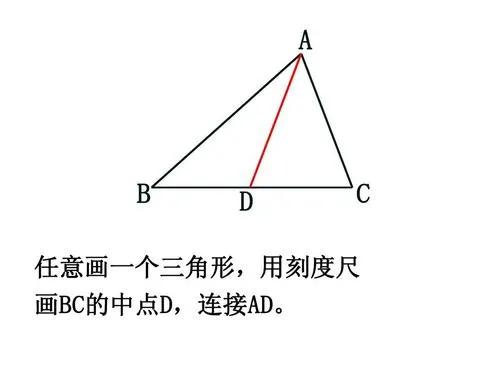
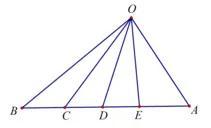
★推广:在三角形中，连接一个顶点和它所对的边的所有n等分点（即:将边平均分成n部分所有的点）线段，会形成n个面积相等的小三角形（面积都为S÷n）

如图所示:

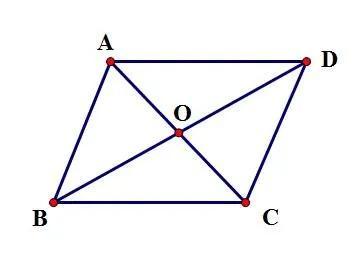
❷对角线:平行四边形的对角线将平行四边形面积分成了两个面积相等的三角形；平行四边形的2条对角线将平行四边形面积分成了4个面积相等的三角形。

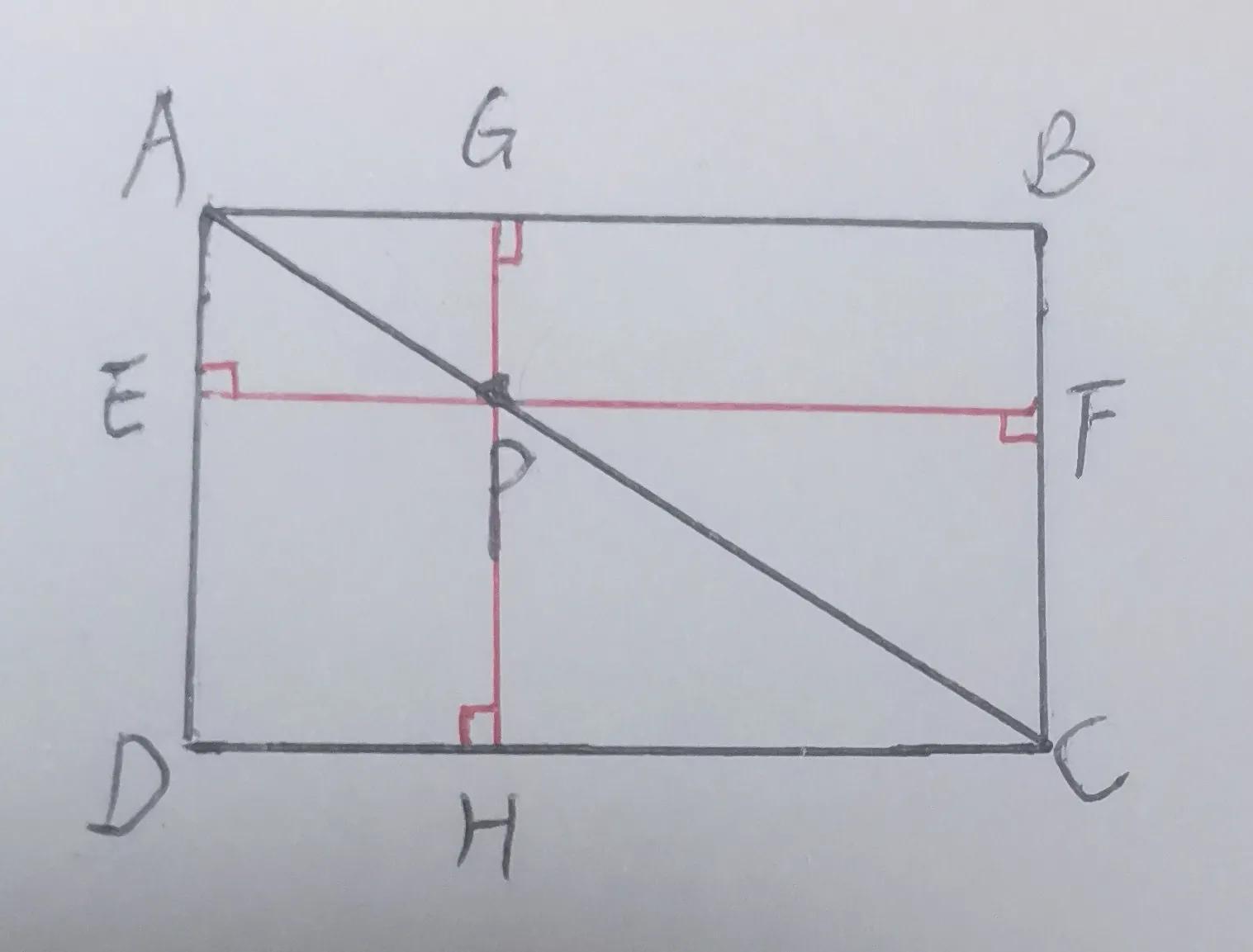
❸垂线段:在长方形的对角线上任取一点，向长方形的四条边做垂线，会形成多组面积相等的三角形和长方形。

❹平行线:两条平行线之间夹的图形(顶点都在两条平行线上)高相等，如果底再相同或相等，则面积也相等。